Geodesic-preserving polygon simplification

O. Aichholzer, T. Hackl, M. Korman, A. Pilz, and B. Vogtenhuber

Abstract:

Polygons are a paramount data structure in computational geometry. While the complexity of many algorithms on simple polygons or polygons with holes depends on the size of the input polygon, the intrinsic complexity of the problems these algorithms solve is often related to the reflex vertices of the polygon. 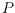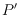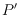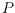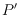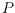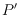In this paper, we give an easy-to-describe linear-time method to replace an input polygon $P$ by a polygon $P'$ such that (1) $P'$ contains $P$, (2) $P'$ has its reflex vertices at the same positions as $P$, and (3) the number of vertices of $P'$ is linear in the number of reflex vertices. 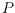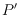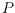Since the solutions of numerous problems on polygons (including shortest paths, geodesic hulls, separating point sets, and Voronoi diagrams) are equivalent for both $P$ and $P'$, our algorithm can be used as a preprocessing step for several algorithms and makes their running time dependent on the number of reflex vertices rather than on the size of $P$.

Reference: O. Aichholzer, T. Hackl, M. Korman, A. Pilz, and B. Vogtenhuber. Geodesic-preserving polygon simplification. Int'l Journal of Computational Geometry & Applications, 24(4):307-323, 2014.