Triangulations Without Pointed Spanning Trees

O. Aichholzer, C. Huemer, and H. Krasser

Abstract:

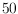
Problem $50$ in the Open Problems Project [#!OPP!#] asks whether any triangulation on a point set in the plane contains a pointed spanning tree as a subgraph. We provide a counterexample. As a consequence we show that there exist triangulations which require a linear number of edge flips to become Hamiltonian.

Reference: O. Aichholzer, C. Huemer, and H. Krasser. Triangulations without pointed spanning trees. Computational Geometry: Theory and Applications, 40(1):79-83, 2008.