Straight Skeletons by Means of Voronoi Diagrams Under Polyhedral
Distance Functions
O. Aichholzer, T. Hackl, S. Huber, and B. Vogtenhuber
Abstract:
We consider the question under which circumstances the straight skeleton and
the Voronoi diagram of a given input shape coincide. More precisely, we
investigate convex distance functions that stem from centrally symmetric
convex polyhedra as unit balls and derive sufficient and necessary conditions
for input shapes in order to obtain identical straight skeletons and Voronoi
diagrams with respect to this distance function. This allows us to present a
new approach for generalizing straight skeletons by means of Voronoi
diagrams, so that the straight skeleton changes continuously when vertices of
the input shape are dislocated, that is, no discontinuous changes as in the
Euclidean straight skeleton occur.
Reference: O. Aichholzer, T. Hackl, S. Huber, and B. Vogtenhuber.
Straight skeletons by means of voronoi diagrams under polyhedral distance
functions.
In Proc. 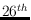 Annual Canadian Conference on Computational Geometry
(CCCG 2014), page online, Halifax, Nova Scotia, Canada, 2014.
Annual Canadian Conference on Computational Geometry
(CCCG 2014), page online, Halifax, Nova Scotia, Canada, 2014.
www-data,
2020-09-10