Plane Graphs with Parity Constraints

O. Aichholzer, T. Hackl, M. Hoffmann, A. Pilz, G. Rote, B. Speckmann, and B. Vogtenhuber

Abstract:

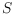
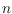
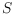
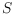
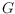
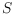
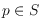
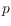
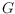
Let $S$ be a set of $n$ points in general position in the plane. Together with $S$ we are given a set of parity constraints, that is, every point of $S$ is labeled either even or odd. A graph $G$ on $S$ satisfies the parity constraint of a point $p \in S$, if the parity of the degree of $p$ in $G$ matches its label. In this paper we study how well various classes of planar graphs can satisfy arbitrary parity constraints. Specifically, we show that we can always find a plane tree, a two-connected outerplanar graph, or a pointed pseudo-triangulation which satisfy all but at most three parity constraints. With triangulations we can satisfy about 2/3 of all parity constraints. 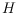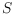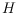In contrast, for a given simple polygon $H$ with polygonal holes on $S$, we show that it is NP-complete to decide whether there exists a triangulation of $H$ that satisfies all parity constraints.

Reference: O. Aichholzer, T. Hackl, M. Hoffmann, A. Pilz, G. Rote, B. Speckmann, and B. Vogtenhuber. Plane graphs with parity constraints. In Lecture Notes in Computer Science (LNCS), Proc. $11^{th}$ International Workshop on Algorithms and Data Structures (WADS), volume 5664, pages 13-24, Banff, Alberta, Canada, 2009.