Large bichromatic point sets admit empty monochromatic $4$-gons

O. Aichholzer, T. Hackl, C. Huemer, F. Hurtado, and B. Vogtenhuber

Abstract:

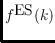
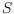
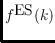
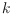
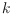
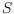
We consider a variation of a problem stated by Erdös and Szekeres in 1935 about the existence of a number $f^\textrm{ES}(k)$ such that any set $S$ of at least $f^\textrm{ES}(k)$ points in general position in the plane has a subset of $k$ points that are the vertices of a convex $k$-gon. In our setting the points of $S$ are colored, and we say that a (not necessarily convex) spanned polygon is monochromatic if all its vertices have the same color. 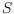Moreover, a polygon is called empty if it does not contain any points of $S$ in its interior. 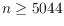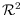We show that any bichromatic set of $n \geq 5044$ points in $\mathcal{R}^2$ in general position determines at least one empty, monochromatic quadrilateral (and thus linearly many).

Reference: O. Aichholzer, T. Hackl, C. Huemer, F. Hurtado, and B. Vogtenhuber. Large bichromatic point sets admit empty monochromatic $4$-gons. In Proc. $25^{th}$ European Workshop on Computational Geometry EuroCG '09, pages 133-136, Brussels, Belgium, 2009.