Maximizing Maximal Angles for Plane Straight Line Graphs

O. Aichholzer, T. Hackl, M. Hoffmann, C. Huemer, A. Pór, F. Santos, B. Speckmann, and B. Vogtenhuber

Abstract:

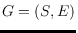
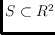
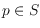
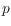
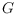
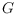
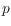
Let $G=(S, E)$ be a plane straight line graph on a finite point set $S\subset {R}^2$ in general position. For a point $p\in S$ let the maximum incident angle of $p$ in $G$ be the maximum angle between any two edges of $G$ that appear consecutively in the circular order of the edges incident to $p$. A plane straight line graph is called 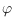$\varphi$-open if each vertex has an incident angle of size at least $\varphi$. 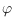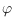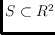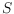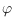In this paper we study the following type of question: What is the maximum angle $\varphi$ such that for any finite set $S\subset {R}^2$ of points in general position we can find a graph from a certain class of graphs on $S$ that is $\varphi$-open? 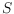In particular, we consider the classes of triangulations, spanning trees, and paths on $S$ and give tight bounds in all but one cases.

Reference: O. Aichholzer, T. Hackl, M. Hoffmann, C. Huemer, A. Pór, F. Santos, B. Speckmann, and B. Vogtenhuber. Maximizing maximal angles for plane straight line graphs. Computational Geometry: Theory and Applications, 46(1):17-28, 2013.