On the number of plane geometric graphs

O. Aichholzer, T. Hackl, C. Huemer, F. Hurtado, H. Krasser, and B. Vogtenhuber

Abstract:

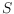
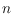
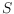
We investigate the number of plane geometric, i.e., straight-line, graphs, a set $S$ of $n$ points in the plane admits. We show that the number of plane geometric graphs and connected plane geometric graphs as well as the number of cycle-free plane geometric graphs is minimized when $S$ is in convex position. Moreover, these results hold for all these graphs with an arbitrary but fixed number of edges. Consequently, we provide a unified proof that the cardinality of any family of acyclic graphs (for example spanning trees, forests, perfect matchings, spanning paths, and more) is minimized for point sets in convex position. In addition we construct a new extremal configuration, the so-called double zig-zag chain. 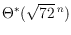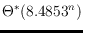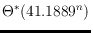Most noteworthy this example bears $\Theta^*(\sqrt{72}\,^n)$ = $\Theta^*(8.4853^n)$ triangulations and $\Theta^*(41.1889^n)$ plane graphs (omitting polynomial factors in both cases), improving the previously known best maximizing examples.

Reference: O. Aichholzer, T. Hackl, C. Huemer, F. Hurtado, H. Krasser, and B. Vogtenhuber. On the number of plane geometric graphs. Graphs and Combinatorics (Springer), 23(1):67-84, 2007.