A fast method for modulus reduction in Residue Number System

O. Aichholzer and H. Hassler

Abstract:

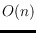
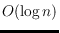
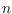
Over the last three decades there has been considerable interest in the implementation of digital computer elements using hardware based on the residue number system. We propose a technique to compute a residue in this number system using a parallel network. Our technique enables scaling, to. We improve a former result of $O(n)$ cycles to $O(\log n)$, where $n$ is the number of moduli. The hardware expense is the same, $O(n^2)$. 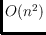Further advantages are that scaling factors can be chosen almost freely allowing scaling with radix $2$. 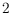Negative numbers are covered as well, requiring no additional effort. Applications are RSA encryption and scaling.

Reference: O. Aichholzer and H. Hassler. A fast method for modulus reduction in residue number system. In Proc. epp'93, pages 41-54, Vienna, Austria, 1993. [IIG-Report-Series 312, TU Graz, Austria, 1991].