Plane paths in simple drawings of complete graphs

O. Aichholzer, A. García, J. Tejel, B. Vogtenhuber, and A. Weinberger

Abstract:

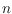
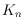
Simple drawings are drawings of graphs in the plane such that vertices are distinct points in the plane, edges are Jordan arcs connecting their endpoints, and edges intersect at most once either in a proper crossing or in a shared endpoint. It is conjectured that every simple drawing of the complete graph with $n$ vertices, $K_n$, contains a plane Hamiltonian cycle, and consequently a plane Hamiltonian path. 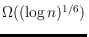However, to the best of our knowledge, $\Omega((\log n)^{1/6})$ is currently the best known lower bound for the length of a plane path contained in any simple drawing of $K_n$. 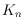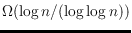We improve this bound to $\Omega(\log n / (\log \log n) )$.

Reference: O. Aichholzer, A. García, J. Tejel, B. Vogtenhuber, and A. Weinberger. Plane paths in simple drawings of complete graphs. In Proc. XIX Encuentros de Geometría Computacional, page 4, 2021.