Plane Matchings in Simple Drawings of Complete Graphs

O. Aichholzer, A. García, J. Tejel, B. Vogtenhuber, and A. Weinberger

Abstract:

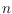
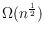
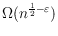
Simple drawings are drawings of graphs in which the edges are Jordan arcs and each pair of edges shares at most one point (a proper crossing or a common endpoint). We show that every simple drawing of the complete graph with $n$ vertices contains  $\Omega(n^{\frac{1}{2}})$ pairwise disjoint edges. 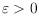This improves the currently known best lower bound $\Omega(n^{\frac{1}{2}-\varepsilon})$ for any $\varepsilon>0$ by Ruiz-Vargas.

Reference: O. Aichholzer, A. García, J. Tejel, B. Vogtenhuber, and A. Weinberger. Plane matchings in simple drawings of complete graphs. In Proceedings of the Computational Geometry: Young Researchers Forum, pages 6-10, 2021.