Simple Drawings of $K_{m,n}$ Contain Shooting Stars

O. Aichholzer, A. García, I. Parada, B. Vogtenhuber, and A. Weinberger

Abstract:

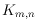
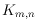
Simple drawings are drawings of graphs in which all edges have at most one common point (either a common endpoint, or a proper crossing). It has been an open question whether every simple drawing of a complete bipartite graph $K_{m,n}$ contains a plane spanning tree as a subdrawing. 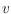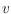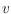We answer this question to the positive by showing that for every simple drawing of $K_{m,n}$ and for every vertex $v$ in that drawing, the drawing contains a shooting star rooted at $v$, that is, a plane spanning tree with all incident edges of $v$.

Reference: O. Aichholzer, A. García, I. Parada, B. Vogtenhuber, and A. Weinberger. Simple drawings of $K_{m,n}$ contain shooting stars. In Proceedings of the 36th European Workshop on Computational Geometry (EuroCG$$2020), pages 36:1-36:7, Würzburg, Germany, 2020.