On the Triangle Vector

O. Aichholzer, R. Fabila-Monroy, and J. Obmann

Abstract:

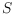
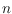
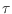
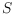
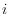
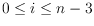
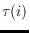
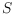
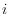
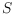
Let $S$ be a set of $n$ points in the plane in general position. In this note we study the so-called triangle vector $\tau$ of $S$. For each cardinality $i$, $0 \leq i \leq n-3$, $\tau(i)$ is the number of triangles spanned by points of $S$ which contain exactly $i$ points of $S$ in their interior. 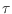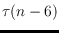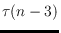We show relations of this vector to other combinatorial structures and derive tight upper bounds for several entries of $\tau$, including $\tau(n-6)$ to $\tau(n-3)$.

Reference: O. Aichholzer, R. Fabila-Monroy, and J. Obmann. On the triangle vector. In Proc. XVIII Encuentros de Geometría Computacional, pages 55-58, Girona, Spain, 2019.