O. Aichholzer, R. Fabila-Monroy, P. Kindermann, I. Parada, R. Paul,
D. Perz, P. Schnider, and B. Vogtenhuber
In this paper, we analyze the number of straight-line perfect matchings with
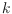
crossings on point sets of size
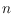
=
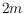
in general position. We show
that for every
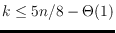
, every
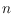
-point set admits a perfect
matching with exactly
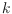
crossings and that there exist
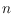
-point sets where
every perfect matching has fewer than
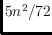
crossings. We also study the
number of perfect matchings with at most
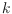
crossings. Finally we show that
convex point sets matchings with
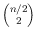
crossings and
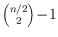
crossings.