Order types and cross-sections of line arrangements in $R^3$

O. Aichholzer, R. Fabila-Monroy, F. Hurtado, P. Perez-Lantero, A. J. Ruiz-Vargas, J. Urrutia, and B. Vogtenhuber

Abstract:

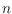
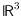
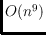
We consider sets of $n$ labeled lines in general position in ${{\sf l} \kern -.10em {\sf R} }^3$, and study the order types of point sets that stem from the intersections of the lines with (directed) planes, not parallel to any given line. As a main result we show that the number of different order types that can be obtained as cross-sections of these lines is $O(n^9)$, and that this bound is tight.

Reference: O. Aichholzer, R. Fabila-Monroy, F. Hurtado, P. Perez-Lantero, A. J. Ruiz-Vargas, J. Urrutia, and B. Vogtenhuber. Order types and cross-sections of line arrangements in $r^3$. In Proc. $26^{th}$ Annual Canadian Conference on Computational Geometry CCCG 2014, page online, Halifax, Nova Scotia, Canada, 2014.