O. Aichholzer, R. Fabila-Monroy, F. Hurtado, P. Perez-Lantero,
A. J. Ruiz-Vargas, J. Urrutia, and B. Vogtenhuber
We consider sets
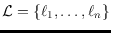
of

labeled
lines in general position in
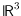
, and study
the order types of point sets
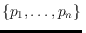
that stem from the
intersections of the lines in
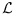
with (directed) planes

, not
parallel to any line of
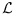
, that is, the proper cross-sections of
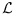
. As two main results, we show that the number of different
order types that can be obtained as cross-sections of
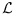
is
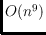
when considering all possible planes

, and
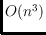
when
restricting considerations to sets of pairwise parallel planes, where both
bounds are tight. The result for parallel planes implies that any set of

points in
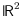
moving with constant (but
possibly different) speeds along straight lines forms at most
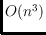
different order types over time. We further generalize the setting from
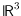
to
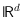
with
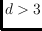
, showing that the number of order types that can be obtained as
cross-sections of a set of

labeled
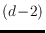
-flats in
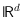
with planes is
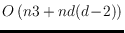
.