Blocking Delaunay Triangulations

O. Aichholzer, R. Fabila-Monroy, T. Hackl, M. van Kreveld, A. Pilz, P. Ramos, and B. Vogtenhuber

Abstract:

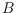
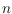
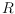
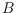
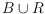
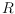
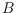
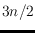
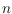
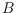
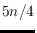
Given a set $B$ of $n$ blue points in general position, we say that a set of red points $R$ blocks $B$ if in the Delaunay triangulation of $B\cup R$ there is no edge connecting two blue points. 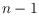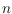We give the following bounds for the size of the smallest set $R$ blocking $B$: (i) $3n/2$ red points are always sufficient to block a set of $n$ blue points, (ii) if $B$ is in convex position, $5n/4$ red points are always sufficient to block it, and (iii) at least $n-1$ red points are always necessary, and there exist sets of blue points that require at least $n$ red points to be blocked.

Reference: O. Aichholzer, R. Fabila-Monroy, T. Hackl, M. van Kreveld, A. Pilz, P. Ramos, and B. Vogtenhuber. Blocking delaunay triangulations. Computational Geometry: Theory and Applications, 46(2):154-159, 2013.