Lower bounds for the number of small convex $k$-holes

O. Aichholzer, R. Fabila-Monroy, T. Hackl, C. Huemer, A. Pilz, and B. Vogtenhuber

Abstract:

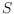
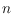
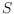
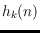
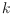
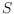
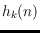
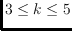
Let $S$ be a set of $n$ points in the plane in general position, that is, no three points of $S$ are on a line. We consider an Erdos-type question on the least number $h_k(n)$ of convex $k$-holes in $S$, and give improved lower bounds on $h_k(n)$, for $3\leq k\leq 5$. 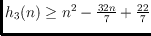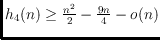Specifically, we show that $h_{3}(n) \geq n^2 - \frac{32n}{7} + \frac{22}{7}$, $h_{4}(n) \geq \frac{n^2}{2} - \frac{9n}{4} - o(n)$, and $h_5(n) \geq \frac{3n}{4} - o(n)$. 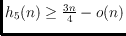We further settle several questions on sets of 12 points posed by Dehnhardt in 1987.

Reference: O. Aichholzer, R. Fabila-Monroy, T. Hackl, C. Huemer, A. Pilz, and B. Vogtenhuber. Lower bounds for the number of small convex $k$-holes. Computational Geometry: Theory and Applications, 47(5):605-613, 2014.