O. Aichholzer, R. Fabila-Monroy, T. Hackl, C. Huemer, and J. Urrutia
Let
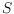
be a
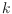
-colored (finite) set of
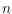
points in
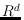
,
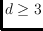
, in
general position, that is, no
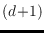
points of
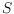
lie in a
common
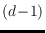
-dimensional hyperplane. We count the number of
empty monochromatic
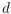
-simplices determined by
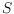
, that is, simplices which
have only points from one color class of
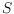
as vertices and no points of
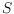
in their interior. For
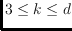
we provide a lower bound of
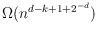
and strengthen this to
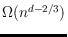
for
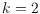
. On the way we provide various results on triangulations of point sets
in
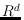
. In particular, for any constant dimension
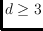
, we prove that
every set of
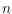
points (
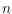
sufficiently large), in general position in
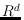
, admits a triangulation with at least
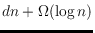
simplices.