On $k$-Gons and $k$-Holes in Point Sets

O. Aichholzer, R. Fabila-Monroy, H. Gonzalez-Aguilar, T. Hackl, M. A. Heredia, C. Huemer, J. Urrutia, P. Valtr, and B. Vogtenhuber

Abstract:

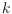
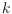
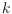
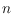
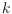
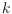
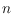
We consider a variation of the classical Erdoos-Szekeres problems on the existence and number of convex $k$-gons and $k$-holes (empty $k$-gons) in a set of $n$ points in the plane. Allowing the $k$-gons to be non-convex, we show bounds and structural results on maximizing and minimizing their numbers. 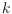Most noteworthy, for any $k$ and sufficiently large $n$, we give a quadratic lower bound for the number of $k$-holes, and show that this number is maximized by sets in convex position. We also provide an improved lower bound for the number of convex 6-holes.

Reference: O. Aichholzer, R. Fabila-Monroy, H. Gonzalez-Aguilar, T. Hackl, M. A. Heredia, C. Huemer, J. Urrutia, P. Valtr, and B. Vogtenhuber. On $k$-gons and $k$-holes in point sets. In Proc. $23^{rd}$ Annual Canadian Conference on Computational Geometry CCCG 2011, pages 21-26, Toronto, Canada, 2011.