4-Holes in Point Sets

O. Aichholzer, R. Fabila-Monroy, H. González-Aguilar, T. Hackl, M. Heredia, C. Huemer, J. Urrutia, and B. Vogtenhuber

Abstract:

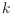
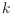
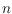
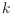
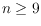
We consider a variant of a question of Erdos on the number of empty $k$-gons ($k$-holes) in a set of $n$ points in the plane, where we allow the $k$-gons to be non-convex. We show bounds and structural results on maximizing and minimizing the number of general 4-holes, and maximizing the number of non-convex 4-holes. 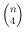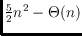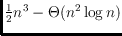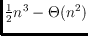In particular, we show that for $n\geq 9$, the maximum number of general 4-holes is ${n \choose 4}$, the minimum number of general 4-holes is at least $\frac{5}{2}n^2 - \Theta(n)$, and the maximum number of non-convex 4-holes is at least $\frac{1}{2}n^3-\Theta(n^2\log n)$ and at most $\frac{1}{2}n^3-\Theta(n^2)$.

Reference: O. Aichholzer, R. Fabila-Monroy, H. González-Aguilar, T. Hackl, M. Heredia, C. Huemer, J. Urrutia, and B. Vogtenhuber. 4-Holes in point sets. Computational Geometry: Theory and Applications, 47(6):644-650, 2014. Special Issue on the 27th European Workshop on Computational Geometry (EuroCG 2011).