Minimization and Maximization Versions of the Quadratic Traveling Salesman Problem

O. Aichholzer, A. Fischer, F. F. J. Meier, U. Pferschy, A. Pilz, and R. Stanek

Abstract:

The traveling salesman problem (TSP) asks for a shortest tour through all vertices of a graph with respect to the weights of the edges. The symmetric quadratic traveling salesman problem (SQTSP) associates a weight with every three vertices traversed in succession. If these weights correspond to the turning angles of the tour, we speak of the angular-metric traveling salesman problem (Angle TSP). In this paper, we first consider the SQTSP from a computational point of view. In particular, we apply a rather basic algorithmic idea and perform the separation of the classical subtour elimination constraints on integral solutions only. Surprisingly, it turns out that this approach is faster than the standard fractional separation procedure known from the literature. We also test the combination with strengthened subtour elimination constraints for both variants, but these turn out to slow down the computation. Secondly, we provide a completely different, mathematically interesting MILP linearization for the Angle TSP that needs only a linear number of additional variables while the standard linearization requires a cubic one. For medium sized instances of a variant of the Angle TSP this formulation yields reduced running times. However, for larger instances or pure Angle TSP instances the new formulation takes more time to solve than the known standard model. Finally, we introduce MaxSQTSP, the maximization version of the quadratic traveling salesman problem. Here it turns out that using some of the stronger subtour elimination constraints helps. For the special case of the MaxAngle TSP we can observe an interesting geometric property if the number of vertices is odd. We show that the sum of inner turning angles in an optimal solution always equals $\pi$. 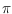This implies that the problem can be solved by the standard ILP model without producing any integral subtours. Moreover, we give a simple constructive polynomial time algorithm to find such an optimal solution. 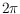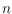If the number of vertices is even the optimal value lies between 0 and $2\pi$ and these two bounds are tight, which can be shown by an analytic solution for a regular $n$-gon.

Reference: O. Aichholzer, A. Fischer, F. F. J. Meier, U. Pferschy, A. Pilz, and R. Stanek. Minimization and maximization versions of the quadratic traveling salesman problem. OPTIMIZATION, 66(4):521-546, 2017.