O. Aichholzer, R. Fabila-Monroy, A. Fuchs, C. Hidalgo-Toscano,
I. Parada, B. Vogtenhuber, and F. Zaragoza
Let
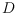
be a straight-line drawing of a graph. The rectilinear 2-colored
crossing number of
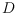
is the minimum number of crossings between edges of
the same color, taken over all possible 2-colorings of the edges of
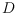
.
First, we show lower and upper bounds on the rectilinear 2-colored crossing
number for the complete graph
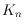
. To obtain this result, we prove that
asymptotic bounds can be derived from optimal and near-optimal instances with
few vertices. We obtain such instances using a combination of heuristics and
integer programming. Second, for any fixed drawing of
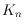
, we improve the
bound on the ratio between its rectilinear 2-colored crossing number and its
rectilinear crossing number.