On the 2-Colored Crossing Number

O. Aichholzer, R. F. Monroy, A. Fuchs, C. H. Toscano, I. Parada, B. Vogtenhuber, and F. Zaragoza

Abstract:

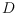
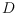
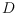
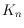
Let $D$ be a straight-line drawing of a graph where every edge is colored with one of two possible colors. The rectilinear 2-colored crossing number of $D$ is the minimum number of crossings between edges of the same color, taken over all possible colorings of $D$. We show lower and upper bounds on the rectilinear 2-colored crossing number for the complete graph $K_n$. 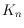Moreover, for fixed drawings of $K_n$ we give bounds on the relation between its rectilinear 2-colored crossing number and its rectilinear crossing number.

Reference: O. Aichholzer, R. F. Monroy, A. Fuchs, C. H. Toscano, I. Parada, B. Vogtenhuber, and F. Zaragoza. On the 2-colored crossing number. In Proc. $35^{th}$ European Workshop on Computational Geometry EuroCG '19, pages 56:1-56:7, Utrecht, The Netherlands, 2019.