Modem Illumination of Monotone Polygons

O. Aichholzer, R. Fabila-Monroy, D. Flores-Peñaloza, T. Hackl, J. Urrutia, and B. Vogtenhuber

Abstract:

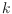
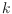
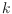
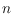
We study a generalization of the classical problem of illumination of polygons. Instead of modeling a light source we model a wireless device whose radio signal can penetrate a given number $k$ of walls. We call these objects $k$-modems and study the minimum number of $k$-modems necessary to illuminate monotone and monotone orthogonal polygons. 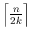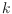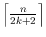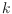We show that every monotone polygon on $n$ vertices can be illuminated with $\left\lceil \frac{n}{2k} \right\rceil$ $k$-modems and exhibit examples of monotone polygons requiring $\left\lceil \frac{n}{2k+2} \right\rceil$ $k$-modems. 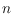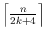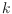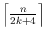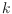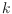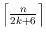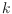For monotone orthogonal polygons, we show that every such polygon on $n$ vertices can be illuminated with $\left\lceil \frac{n}{2k+4} \right\rceil$ $k$-modems and give examples which require $\left\lceil \frac{n}{2k+4} \right\rceil$ $k$-modems for $k$ even and $\left\lceil \frac{n}{2k+6} \right\rceil$ for $k$ odd.

Reference: O. Aichholzer, R. Fabila-Monroy, D. Flores-Peñaloza, T. Hackl, J. Urrutia, and B. Vogtenhuber. Modem illumination of monotone polygons. Computational Geometry: Theory and Applications, 68:101-118, 2018. Special Issue in Memory of Ferran Hurtado.