Empty Monochromatic Triangles

O. Aichholzer, R. Fabila-Monroy, D. Flores-Peñaloza, T. Hackl, C. Huemer, and J. Urrutia

Abstract:

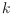
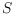
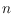
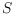
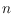
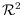
We consider a variation of a problem stated by Erdös and Guy in 1973 about the number of convex $k$-gons determined by any set $S$ of $n$ points in the plane. In our setting the points of $S$ are colored and we say that a spanned polygon is monochromatic if all its points are colored with the same color. 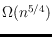As a main result we show that any bi-colored set of $n$ points in $\mathcal{R}^2$ in general position determines a super-linear number of empty monochromatic triangles, namely $\Omega(n^{5/4})$.

Reference: O. Aichholzer, R. Fabila-Monroy, D. Flores-Peñaloza, T. Hackl, C. Huemer, and J. Urrutia. Empty monochromatic triangles. Computational Geometry: Theory and Applications, 42(9):934-938, 2009.