O. Aichholzer, F. Ebenführer, I. Parada, A. Pilz, and
B. Vogtenhuber
In this work we study rotation systems and semi-simple drawings of
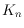
. A
simple drawing of a graph is a drawing in which every pair of edges
intersects in at most one point. In a semi-simple drawing, edge pairs might
intersect in multiple points, but incident edges only intersect in their
common endpoint. A rotation system is called (semi-)realizable if it can be
realized with a (semi-)simple drawing. It is known that a rotation system is
realizable if and only if all its 5-tuples are realizable. For the problem of
characterizing semi-realizability, we present a rotation system with six
vertices that is not semi-realizable, although all its 5-tuples are
semi-realizable. Moreover, by an exhaustive computer search, we show that
also for seven vertices there exist minimal not semi-realizable rotation
systems (that is, rotation systems in which all proper sub-rotation systems
are semi-realizable). This indicates that checking semi-realizability is
harder than checking realizability. Finally we show that for semi-simple
drawings, generalizations of Conway's Thrackle Conjecture and the conjecture
on the existence of plane Hamiltonian cycles do not hold.