Geometric Dominating Sets - A Minimum Version of the No-Three-In-Line Problem

O. Aichholzer, D. Eppstein, and E.-M. Hainzl

Abstract:

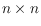
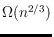
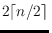
We consider a minimizing variant of the well-known No-Three-In-Line Problem, the Geometric Dominating Set Problem: What is the smallest number of points in an $n\times n$ grid such that every grid point lies on a common line with two of the points in the set? We show a lower bound of $\Omega(n^{2/3})$ points and provide a constructive upper bound of size $2 \lceil n/2 \rceil$. If the points of the dominating sets are required to be in general position we provide optimal solutions for grids of size up to $12 \times 12$. 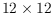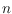For arbitrary $n$ the currently best upper bound remains the obvious $2n$. 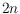Finally, we discuss some further variations of the problem.

Reference: O. Aichholzer, D. Eppstein, and E.-M. Hainzl. Geometric dominating sets - a minimum version of the no-three-in-line problem. In Proceedings of the 37th European Workshop on Computational Geometry (EuroCG$\,$2021), pages 17:1-17:7, St. Petersburg, Germany, 2021.