A Simple Linear Time Greedy Triangulation Algorithm for Uniformly Distributed Points

O. Aichholzer, R. Drysdale, and G. Rote

Abstract:

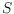
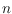
The greedy triangulation (GT) of a set $S$ of $n$ points in the plane is the triangulation obtained by starting with the empty set and at each step adding the shortest compatible edge between two of the points, where a compatible edge is defined to be an edge that crosses none of the previously added edges. 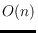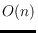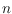In this paper we present a simple, practical algorithm that computes the greedy triangulation in expected time $O(n)$ and space $O(n)$, for $n$ points drawn independently from a uniform distribution over some fixed convex shape.
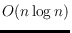
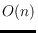
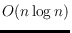
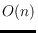
This algorithm is an improvement of the $O(n \log n)$ algorithm of Dickerson, Drysdale, McElfresh, and Welzl. It uses their basic approach, but generates only $O(n)$ plausible greedy edges instead of $O(n \log n)$. It uses some ideas similar to those presented in Levcopoulos and Lingas's $O(n)$ expected time algorithm. Since we use more knowledge about the structure of a random point set and its greedy triangulation, our algorithm needs only elementary data structures and simple bucketing techniques. Thus it is a good deal simpler to explain and to implement than the algorithm of Levcopoulos and Lingas.

Reference: O. Aichholzer, R. Drysdale, and G. Rote. A simple linear time greedy triangulation algorithm for uniformly distributed points. IIG-Report-Series 408, TU Graz, Austria, 1995. Presented at the Workshop on Computational Geometry, Army MSI Cornell, Stony Brook, 1994.