O. Aichholzer, E. D. Demaine, M. Korman, A. Lubiw, J. Lynch,
Z. Masárová, M. Rudoy, V. Vassilevska Williams, and N. Wein
Given a graph where every vertex has exactly one labeled token, how can we most
quickly execute a given permutation on the tokens? In (sequential) token
swapping, the goal is to use the shortest possible sequence of swaps, each of
which exchanges the tokens at the two endpoints of an edge of the graph. In
parallel token swapping, the goal is to use the fewest rounds, each of which
consists of one or more swaps on the edges of a matching. We prove that both
of these problems remain NP-hard when the graph is restricted to be a tree.
These token swapping problems have been studied by disparate groups of
researchers in discrete mathematics, theoretical computer science, robot
motion planning, game theory, and engineering. Previous work establishes
NP-completeness on general graphs (for both problems); polynomial-time
algorithms for simple graph classes such as cliques, stars, paths, and
cycles; and constant-factor approximation algorithms in some cases. The two
natural cases of sequential and parallel token swapping in trees were first
studied over thirty years ago (as "sorting with a transposition tree") and
over twenty-five years ago (as "routing permutations via matchings"), yet
their complexities were previously unknown. We also show limitations on
approximation of sequential token swapping on trees: we identify a broad
class of algorithms that encompass all three known polynomial-time algorithms
that achieve the best known approximation factor (which is
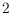
) and show that
no such algorithm can achieve an approximation factor less than
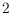
.