Erdos-Szekeres-Type Games

O. Aichholzer, J. M. Díaz-Báñez, T. Hackl, D. Orden, A. Pilz, I. Ventura, and B. Vogtenhuber

Abstract:

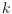
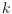
We consider several combinatorial games, inspired by the Erdos-Szekeres theorem that states the existence of a convex $k$-gon in every sufficiently large point set. Two players take turns to place points in the Euclidean plane and the game is over as soon as the first $k$-gon appears. In the Maker-Maker setting the player who placed the last point wins, while in the Avoider-Avoider version this player loses. Combined versions like Maker-Breaker are also possible. 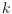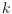Moreover, variants can be obtained by considering that (1) the points to be placed are either uncolored or bichromatic, (2) both players have their own color or can play with both colors, (3) the $k$-gon must be empty of other points, or (4) the $k$-gon has to be convex.

Reference: O. Aichholzer, J. M. Díaz-Báñez, T. Hackl, D. Orden, A. Pilz, I. Ventura, and B. Vogtenhuber. Erdos-szekeres-type games. In Proc. $35^{th}$ European Workshop on Computational Geometry EuroCG '19, pages 23:1-23:7, Utrecht, The Netherlands, 2019.