O. Aichholzer, F. Duque, R. Fabila-Monroy, C. Hidalgo-Toscano, and
O. E. García-Quintero
A drawing of a graph in the plane is
pseudolinear if the edges of the
drawing can be extended to doubly-infinite curves that form an arrangement of
pseudolines, that is, any pair of edges crosses precisely once. A special
case are
rectilinear drawings where the edges of the graph are drawn as
straight line segments. The rectilinear (pseudolinear) crossing number of a
graph is the minimum number of pairs of edges of the graph that cross in any
of its rectilinear (pseudolinear) drawings. In this paper we describe an
ongoing project to continuously obtain better asymptotic upper bounds on the
rectilinear and pseudolinear crossing number of the complete graph
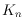
.