O. Aichholzer, J. Cardinal, V. Kusters, S. Langerman, and P. Valtr
We consider the problem of reconstructing the combinatorial structure of a set
of
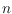
points in the plane given partial information on the relative position
of the points. This partial information consists of the radial ordering, for
each of the
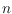
points, of the
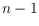
other points around it. We show that
this information is sufficient to reconstruct the chirotope, or labeled order
type, of the point set, provided its convex hull has size at least four.
Otherwise, we show that there can be as many as
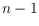
distinct chirotopes
that are compatible with the partial information, and this bound is tight.
Our proofs yield polynomial-time reconstruction algorithms. These results
provide additional theoretical insights on previously studied problems
related to robot navigation and visibility-based reconstruction.