O. Aichholzer, J. Cardinal, T. Huynh, K. Knauer, T. Mütze,
R. Steiner, and B. Vogtenhuber
Flip graphs are a ubiquitous class of graphs, which encode relations on a set
of combinatorial objects by elementary, local changes. Skeletons of
associahedra, for instance, are the graphs induced by quadrilateral flips in
triangulations of a convex polygon. For some definition of a flip graph, a
natural computational problem to consider is the flip distance: Given two
objects, what is the minimum number of flips needed to transform one into the
other? We consider flip graphs on orientations of simple graphs, where flips
consist of reversing the direction of some edges. More precisely, we consider
so-called
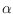
-orientations of a graph
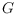
, in which every vertex
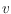
has
a specified outdegree
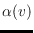
, and a flip consists of reversing all edges
of a directed cycle. We prove that deciding whether the flip distance between
two
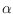
-orientations of a planar graph
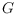
is at most two is
-complete. This also holds in the special case of perfect matchings, where
flips involve alternating cycles. This problem amounts to finding geodesics
on the common base polytope of two partition matroids, or, alternatively, on
an alcoved polytope. It therefore provides an interesting example of a flip
distance question that is computationally intractable despite having a
natural interpretation as a geodesic on a nicely structured combinatorial
polytope. We also consider the dual question of the flip distance between
graph orientations in which every cycle has a specified number of forward
edges, and a flip is the reversal of all edges in a minimal directed cut. In
general, the problem remains hard. However, if we restrict to flips that only
change sinks into sources, or vice-versa, then the problem can be solved in
polynomial time. Here we exploit the fact that the flip graph is the cover
graph of a distributive lattice. This generalizes a recent result from Zhang,
Qian, and Zhang (Acta. Math. Sin.-English Ser., 2019).