Flip distances between graph orientations

O. Aichholzer, J. Cardinal, T. Huynh, K. Knauer, T. Mütze, R. Steiner, and B. Vogtenhuber

Abstract:

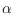
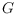
Flip graphs are a ubiquitous class of graphs, which encode relations induced on a set of combinatorial objects by elementary, local changes. A natural computational problem to consider is the flip distance: Given two objects, what is the minimum number of flips needed to transform one into the other? 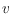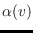We consider flip graphs on so-called $\alpha$-orientations of a graph $G$, in which every vertex $v$ has a specified outdegree $\alpha(v)$, and a flip consists of reversing all edges of a directed cycle. 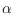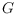We prove that deciding whether the flip distance between two $\alpha$-orientations of a planar graph $G$ is at most 2 is -complete. This also holds in the special case of plane perfect matchings, where flips involve alternating cycles. We also consider the dual question of the flip distance between graph orientations in which every cycle has a specified number of forward edges, and a flip is the reversal of all edges in a minimal directed cut. In general, the problem remains hard, but if we only change sinks into sources, or vice-versa, then the problem can be solved in polynomial time.

Reference: O. Aichholzer, J. Cardinal, T. Huynh, K. Knauer, T. Mütze, R. Steiner, and B. Vogtenhuber. Flip distances between graph orientations. In 45th International Workshop on Graph-Theoretic Concepts in Computer Science, volume 11789 of Lecture Notes in Computer Science (LNCS), pages 120-134, Vall de Nuria, Spain, 2019.