O. Aichholzer, J. Cardinal, T. Hackl, F. Hurtado, M. Korman, A. Pilz,
R. Silveira, R. Uehara, B. Vogtenhuber, and E. Welzl
We show that in every arrangement of
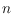
red and blue lines (in general
position and not all of the same color) there is a path through a linear
number of cells where red and blue lines are crossed alternatingly (and no
cell is revisited). When all lines have the same color, and hence the
preceding alternating constraint is dropped, we prove that the dual graph of
the arrangement always contains a path of length
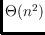
.