O. Aichholzer, S. Cabello, R. Fabila-Monroy, D. Flores-Peñaloza,
T. Hackl, C. Huemer, F. Hurtado, and D. Wood
We study the following extremal problem for geometric graphs: How many
arbitrary edges can be removed from a complete geometric graph with
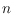
vertices such that the remaining graph still contains a certain non-crossing
subgraph. In particular we consider perfect matchings and subtrees of a given
size. For both classes of geometric graphs we obtain tight bounds on the
maximum number of removable edges. We further present several conjectures and
bounds on the number of removable edges for other classes of non-crossing
geometric graphs.