What makes a Tree a Straight Skeleton?

O. Aichholzer, H. Cheng, S. Devadoss, T. Hackl, S. Huber, B. Li, and A. Risteski

Abstract:

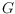
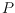
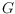
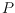
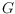
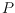
Let $G$ be a cycle-free connected straight-line graph with predefined edge lengths and fixed order of incident edges around each vertex. We address the problem of deciding whether there exists a simple polygon $P$ such that $G$ is the straight skeleton of $P$. We show that for given $G$ such a polygon $P$ might not exist, and if it exists it might not be unique. For the later case we give an example with exponentially many suitable polygons. For small star graphs and caterpillars we show necessary and sufficient conditions for constructing $P$.
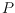
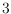
Considering only the topology of the tree, that is, ignoring the length of the edges, we show that any tree whose inner vertices have degree at least $3$ is isomorphic to the straight skeleton of a suitable convex polygon.

Reference: O. Aichholzer, H. Cheng, S. Devadoss, T. Hackl, S. Huber, B. Li, and A. Risteski. What makes a tree a straight skeleton? In Proc. $24^{th}$ Annual Canadian Conference on Computational Geometry CCCG 2012, pages 253-258, Charlottetown, PEI, Canada, 2012.