What makes a Tree a Straight Skeleton?

O. Aichholzer, H. Cheng, S. Devadoss, T. Hackl, S. Huber, B. Li, and A. Risteski

Abstract:

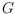
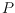
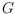
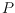
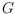
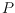
Let $G$ be a cycle-free connected straight-line graph with predefined edge lengths and fixed order of incident edges around each vertex. We address the problem of deciding whether there exists a simple polygon $P$ such that $G$ is the straight skeleton of $P$. We show that for given $G$ such a polygon $P$ might not exist, and if it exists it might not be unique. 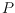For small star graphs and caterpillars we give necessary and sufficient conditions for constructing $P$.

Reference: O. Aichholzer, H. Cheng, S. Devadoss, T. Hackl, S. Huber, B. Li, and A. Risteski. What makes a tree a straight skeleton? In Proc. $28^{th}$ European Workshop on Computational Geometry EuroCG '12, pages 137-140, Assisi, Italy, 2012.