O. Aichholzer, L. Caraballo, J. Díaz-Báñez,
R. Fabila-Monroy, C. Ochoa, and P. Nigsch
Let
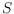
be a set of
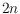
points on a circle such that for each point
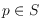
also its antipodal (mirrored with respect to the circle center) point
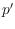
belongs to
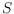
. A polygon
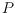
of size
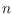
is called
antipodal if it
consists of precisely one point of each antipodal pair
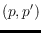
of
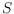
. We
provide a complete characterization of antipodal polygons which maximize
(minimize, respectively) the area among all antipodal polygons of
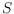
. Based
on this characterization, a simple linear time algorithm is presented for
computing extremal antipodal polygons. Moreover, for the generalization of
antipodal polygons to higher dimensions we show that a similar
characterization does not exist.