Coloring Hypergraphs Induced by Dynamic Point Sets and Bottomless Rectangles

A. Asinowski, J. Cardinal, N. Cohen, S. Collette, T. Hackl, M. Hoffmann, K. Knauer, S. Langerman, M. Lason, P. Micek, G. Rote, and T. Ueckerdt

Abstract:

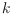
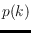
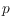
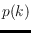
We consider a coloring problem on dynamic, one-dimensional point sets: points appearing and disappearing on a line at given times. We wish to color them with $k$ colors so that at any time, any sequence of $p(k)$ consecutive points, for some function $p$, contains at least one point of each color. We prove that no such function $p(k)$ exists in general. However, in the restricted case in which points appear gradually, but never disappear, we give a coloring algorithm guaranteeing the property at any time with $p(k)=3k-2$. 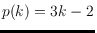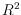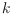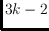This can be interpreted as coloring point sets in ${R}^2$ with $k$ colors such that any bottomless rectangle containing at least $3k-2$ points contains at least one point of each color. Here a bottomless rectangle is an axis-aligned rectangle whose bottom edge is below the lowest point of the set. 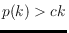For this problem, we also prove a lower bound $p(k)>ck$, where $c>1.67$. 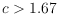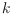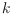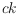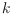Hence, for every $k$ there exists a point set, every $k$-coloring of which is such that there exists a bottomless rectangle containing $ck$ points and missing at least one of the $k$ colors. Chen et al. 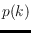(2009) proved that no such function $p(k)$ exists in the case of general axis-aligned rectangles. Our result also complements recent results from Keszegh and Pálvölgyi on cover-decomposability of octants (2011, 2012).

Reference: A. Asinowski, J. Cardinal, N. Cohen, S. Collette, T. Hackl, M. Hoffmann, K. Knauer, S. Langerman, M. Lason, P. Micek, G. Rote, and T. Ueckerdt. Coloring hypergraphs induced by dynamic point sets and bottomless rectangles. In Lecture Notes in Computer Science (LNCS), Proc. $13^{th}$ Algorithms and Data Structures Symposium (WADS 2013), volume 8037, pages 73-84, London, Ontario, Canada, 2013.