Linear Transformation Distance for Bichromatic Matchings

O. Aichholzer, L. Barba, T. Hackl, A. Pilz, and B. Vogtenhuber

Abstract:

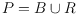
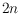
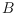
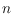
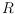
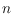
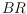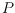
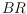
Let $P=B\cup R$ be a set of $2n$ points in general position, where $B$ is a set of $n$ blue points and $R$ a set of $n$ red points. A $BR$-matching is a plane geometric perfect matching on $P$ such that each edge has one red endpoint and one blue endpoint. Two $BR$-matchings are compatible if their union is also plane.
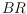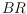
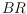
The transformation graph of $BR$-matchings contains one node for each $BR$-matching and an edge joining two such nodes if and only if the corresponding two $BR$-matchings are compatible. In SoCG 2013 it has been shown by Aloupis, Barba, Langerman, and Souvaine that this transformation graph is always connected, but its diameter remained an open question. 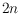In this paper we provide an alternative proof for the connectivity of the transformation graph and prove an upper bound of $2n$ for its diameter, which is asymptotically tight.

Reference: O. Aichholzer, L. Barba, T. Hackl, A. Pilz, and B. Vogtenhuber. Linear transformation distance for bichromatic matchings. Computational Geometry: Theory and Applications, 68:77-88, 2018. Special Issue in Memory of Ferran Hurtado.