Holes in 2-convex point sets

O. Aichholzer, M. Balko, T. Hackl, A. Pilz, P. Ramos, P. Valtr, and B. Vogtenhuber

Abstract:

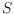
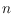
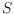
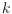
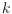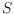
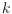
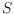
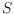
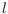
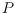
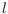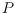
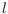
Let $S$ be a set of $n$ points in the plane in general position (no three points from $S$ are collinear). For a positive integer $k$, a $k$-hole in $S$ is a convex polygon with $k$ vertices from $S$ and no points of $S$ in its interior. For a positive integer $l$, a simple polygon $P$ is $l$-convex if no straight line intersects the interior of $P$ in more than $l$ connected components. 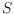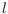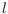A point set $S$ is $l$-convex if there exists an $l$-convex polygonization of $S$. 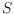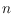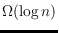Considering a typical Erdos-Szekeres-type problem, we show that every 2-convex point set of size $n$ contains an $\Omega(\log n)$-hole. In comparison, it is well known that there exist arbitrarily large point sets in general position with no 7-hole. 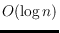Further, we show that our bound is tight by constructing 2-convex point sets with holes of size at most $O(\log n)$.

Reference: O. Aichholzer, M. Balko, T. Hackl, A. Pilz, P. Ramos, P. Valtr, and B. Vogtenhuber. Holes in 2-convex point sets. Computational Geometry: Theory and Applications, 74:38-49, 2018.