A superlinear lower bound on the number of 5-holes

O. Aichholzer, M. Balko, T. Hackl, J. Kyncl, I. Parada, M. Scheucher, P. Valtr, and B. Vogtenhuber

Abstract:

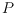
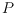
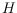
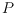
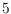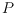
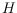
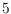
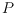
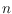
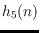
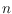
Let $P$ be a finite set of points in the plane in general position, that is, no three points of $P$ are on a common line. We say that a set $H$ of five points from $P$ is a $5$-hole in $P$ if $H$ is the vertex set of a convex $5$-gon containing no other points of $P$. For a positive integer $n$, let $h_5(n)$ be the minimum number of 5-holes among all sets of $n$ points in the plane in general position. 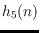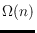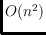Despite many efforts in the last 30 years, the best known asymptotic lower and upper bounds for $h_5(n)$ have been of order $\Omega(n)$ and $O(n^2)$, respectively. 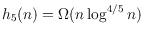We show that $h_5(n) = \Omega(n\log^{4/5}{n})$, obtaining the first superlinear lower bound on $h_5(n)$. 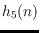The following structural result, which might be of independent interest, is a crucial step in the proof of this lower bound. 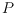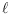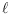If a finite set $P$ of points in the plane in general position is partitioned by a line $\ell$ into two subsets, each of size at least 5 and not in convex position, then $\ell$ intersects the convex hull of some 5-hole in $P$. 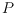The proof of this result is computer-assisted.

Reference: O. Aichholzer, M. Balko, T. Hackl, J. Kyncl, I. Parada, M. Scheucher, P. Valtr, and B. Vogtenhuber. A superlinear lower bound on the number of 5-holes. Journal of Combinatorial Theory A, pages 1-31, 2019. online.