O. Aichholzer, M. Balko, M. Hoffmann, J. Kyncl, W. Mulzer,
I. Parada, A. Pilz, M. Scheucher, P. Valtr, B. Vogtenhuber, and E. Welzl
In order to have a compact visualization of the order type of a given point set
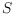
, we are interested in geometric graphs on
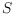
with few edges that
unequivocally display the order type of
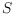
. We introduce the concept of
exit edges, which prevent the order type from changing under
continuous motion of vertices. Exit edges have a natural dual
characterization, which allows us to efficiently compute them and to bound
their number.