Compatible Geometric Matchings

O. Aichholzer, S. Bereg, A. Dumitrescu, A. García, C. Huemer, F. Hurtado, M. Kano, A. Márquez, D. Rappaport, S. Smorodinsky, D. Souvaine, J. Urrutia, and D. Wood

Abstract:

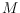
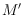
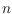
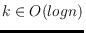
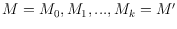
Abstract: This paper studies non-crossing geometric perfect matchings. Two such perfect matchings are compatible if they have the same vertex set and their union is also non-crossing. Our first result states that for any two perfect matchings $M$ and $M'$ of the same set of $n$ points, for some $k \in O(log n)$, there is a sequence of perfect matchings $M = M_0,M_1, . . . 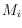,M_k = M'$, such that each $M_i$ is compatible with $M_{i+1}$. 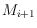This improves the previous best bound of $k \leq n-2$. 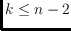We then study the conjecture: every perfect matching with an even number of edges has an edge-disjoint compatible perfect matching. We introduce a sequence of stronger conjectures that imply this conjecture, and prove the strongest of these conjectures in the case of perfec matchings that consist of vertical and horizontal segments. 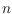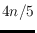Finally, we prove that every perfect matching with $n$ edges has an edge-disjoint compatible matching with approximately $4n/5$ edges.

Reference: O. Aichholzer, S. Bereg, A. Dumitrescu, A. García, C. Huemer, F. Hurtado, M. Kano, A. Márquez, D. Rappaport, S. Smorodinsky, D. Souvaine, J. Urrutia, and D. Wood. Compatible geometric matchings. Electronic Notes in Discrete Mathematics, 31:201-206, 2008.