O. Aichholzer, M. Biro, E. Demaine, M. Demaine, D. Eppstein,
S. P. Fekete, A. Hesterberg, I. Kostitsyna, and C. Schmidt
We study the problem of folding a given polyomino
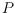
into a polycube
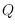
,
allowing faces of
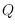
to be covered multiple times. First, we define a
variety of folding models according to whether the folds (a) must be along
grid lines of
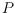
or can divide squares in half (diagonally and/or
orthogonally), (b) must be mountain or can be both mountain and valley,
(c) can remain flat (forming an angle of
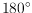
), and (d) whether the
folding must lie on just the polycube surface or can have interior faces as
well. Second, we give all inclusion relations among all models that fold on
the grid lines of
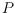
. Third, we characterize all polyominoes that can fold
into a unit cube, in some models. Fourth, we give a linear-time dynamic
programming algorithm to fold a tree-shaped polyomino into a constant-size
polycube, in some models. Finally, we consider the triangular version of the
problem, characterizing which polyiamonds fold into a regular tetrahedron.