Drawing Graphs as Spanners

O. Aichholzer, M. Borrazzo, P. Bose, J. Cardinal, F. Frati, P. Morin, and B. Vogtenhuber

Abstract:

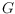
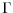
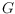
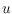
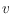
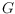
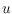
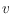
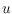
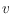
We study the problem of embedding graphs in the plane as good geometric spanners. That is, for a graph $G$, the goal is to construct a straight-line drawing $\Gamma$ of $G$ in the plane such that, for any two vertices $u$ and $v$ of $G$, the ratio between the minimum length of any path from $u$ to $v$ and the Euclidean distance between $u$ and $v$ is small. 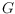The maximum such ratio, over all pairs of vertices of $G$, is the spanning ratio of $\Gamma$. 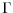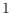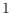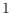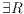First, we show that deciding whether a graph admits a straight-line drawing with spanning ratio $1$, a proper straight-line drawing with spanning ratio $1$, and a planar straight-line drawing with spanning ratio $1$ are NP-complete, $\exists \mathbb R$-complete, and linear-time solvable problems, respectively. 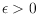Second, we prove that, for every $\epsilon>0$, every (planar) graph admits a proper (resp. planar) straight-line drawing with spanning ratio smaller than $1+\epsilon$. 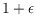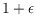Third, we note that our drawings with spanning ratio smaller than $1+\epsilon$ have large edge-length ratio, that is, the ratio between the lengths of the longest and of the shortest edge is exponential. We show that this is sometimes unavoidable. More generally, we identify having bounded toughness as the criterion that distinguishes graphs that admit straight-line drawings with constant spanning ratio and polynomial edge-length ratio from graphs that do not.

Reference: O. Aichholzer, M. Borrazzo, P. Bose, J. Cardinal, F. Frati, P. Morin, and B. Vogtenhuber. Drawing graphs as spanners. Discrete & Computational Geometry, 68:774-795, 06 2022.