Constant-level greedy triangulations approximate the MWT well

O. Aichholzer, F. Aurenhammer, G. Rote, and Y.-F. Xu

Abstract:

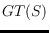
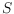
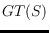
The well-known greedy triangulation $GT(S)$ of a finite point set $S$ is obtained by inserting compatible edges in increasing length order, where an edge is compatible if it does not cross previously inserted ones. Exploiting the concept of so-called light edges, we introduce a definition of $GT(S)$ that does not rely on the length ordering of the edges. 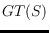Rather, it provides a decomposition of $GT(S)$ into levels, and the number of levels allows us to bound the total edge length of $GT(S)$. 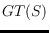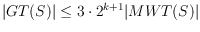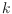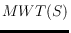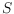In particular, we show $\vert GT(S)\vert \leq 3 \cdot 2^{k+1} \vert MWT(S)\vert$, where $k$ is the number of levels and $MWT(S)$ is the minimum-weight triangulation of $S$.

Reference: O. Aichholzer, F. Aurenhammer, G. Rote, and Y.-F. Xu. Constant-level greedy triangulations approximate the MWT well. In C. Du, Zhang, editor, Proc. $2^{nd}$ Int'l. Symp. Operations Research & Applications ISORA'96, Lecture Notes in Operations Research, volume 2, pages 309-318, Guilin, P. R. China, 1996. World Publishing Corporation.