Triangulations intersect nicely
O. Aichholzer, F. Aurenhammer, G. Rote, and M. Taschwer
Abstract:
We prove that two different triangulations of the same planar point set always
intersect in a systematic manner, concerning both their edges and their
triangles. As a consequence, improved lower bounds on the weight of a
triangulation are obtained by solving an assignment problem. The new bounds
cover the previously known bounds and can be computed in polynomial time. As
a by-product, an easy-to-recognize class of point sets is exhibited where the
minimum-weight triangulation coincides with the greedy triangulation.
Reference: O. Aichholzer, F. Aurenhammer, G. Rote, and M. Taschwer.
Triangulations intersect nicely.
In Proc. 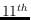 Ann. ACM Symp. Computational Geometry, pages
220-229, Vancouver, Canada, 1995.
Ann. ACM Symp. Computational Geometry, pages
220-229, Vancouver, Canada, 1995.
www-data,
2020-09-10