Hamiltonian meander paths and cycles on bichromatic point sets

O. Aichholzer, C. A. Galicia, I. Parada, A. Pilz, J. Tejel, C. D. Tóth, J. Urrutia, and B. Vogtenhuber

Abstract:

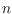
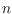
We show that any set of $n$ blue and $n$ red points on a line admits a plane meander path, that is, a crossing-free panning path that passes across the line on red and blue points in alternation. For meander cycles, we derive tight bounds on the minimum number of necessary crossings which depend on the coloring of the points. Finally, we provide some relations for the number of plane meander paths.

Reference: O. Aichholzer, C. A. Galicia, I. Parada, A. Pilz, J. Tejel, C. D. Tóth, J. Urrutia, and B. Vogtenhuber. Hamiltonian meander paths and cycles on bichromatic point sets. In Proc. XVIII Encuentros de Geometría Computacional, pages 35-38, Girona, Spain, 2019.